Think back to your childhood when you were a stress-free kid playing on a playground. Remember climbing up the jungle gym and sliding down the plastic slide? If you weren't careful, you would sometimes rub your elbows on the sides of the slide on the way down, creating painful scrapes on your arms. This was because of friction between you and the slide. Those plastic slides are example applications of inclined planes. An object on a slanted plane experiences gravity due to its weight, causing it to slide down the edge. And as it slides against the plane, it also experiences friction that opposes its motion and slows it down. In this article, we'll learn how to describe and calculate these forces, hopefully avoiding any bumps and bruises on the way!
Fig. 1 - A child sliding down a playground slide experiences the same physics as an object in an inclined plane.
Inclined Plane Definition
An inclined plane is a surface elevated at a certain angle in which we consider the motion of an object.
An inclined plane can be a tricky scenario as we must consider the different components of every applied force.
An inclined plane can be a tricky scenario as we must consider the different components of every applied force.
Let's consider the simplest scenario: a box on a horizontal plane. In this case, we only need to consider two forces: the weight of the box acting downwards and the reaction force from the plane, which is equal and opposite to the weight. As a result, the box remains stationary according to Newton's Second Law.
The weight of a box on a horizontal plane acts perpendicular to the plane. On an inclined plane, this does not happen. But we can split the weight into components parallel and perpendicular to the plane.
Take a look at the figure above. We contrast the situation of the horizontal plane with the inclined plane on the right. For an inclined plane, it is useful to decompose the force into components parallel or perpendicular to the inclined plane we are considering. We can see this decomposition for the weight, appearing as colored arrows in the figure. Note how a weight component pushes the box down the plane while the other does it against the plane surface. Because of these components, a block on an inclined slope slides down without losing contact with the slope. In this article, we will learn how to describe these forces in more mathematical detail while also understanding how friction plays a part in the motion of objects!
Forces on an Inclined Plane
In this section, we will calculate the weight components using trigonometry. But let's see why that is useful.
For an object on a flat surface, the normal force points vertically upwards. It is in the opposite direction of the object's weight because the normal force is a contact force, and thus, it acts perpendicularly to the surface. However, for an object on an inclined plane, the surface is not perpendicular to the force of gravity! Hence, the normal force does not act in the opposite direction to gravity. Instead, it acts perpendicular to the direction of the inclined plane.
In the previous image, we showed the graphic representation for splitting the weight of the object into a component perpendicular to the inclined plane (highlighted in blue) and another component parallel to the inclined plane (highlighted in red). Therefore the normal force won't be equal to the weight but only to the weight's perpendicular component, which pushes the object against the plane.
Now, to calculate these components, it is useful to remember a few important angle properties. Firstly, the sum of all angles in a triangle equals \( 180^\circ \). Secondly, if we have two parallel lines, \( a \) and \( b \), as in the figure below, and you have a transversal line intersecting them, then the corresponding interior angles are congruent. In the figure, the angles \( \alpha \) and \( \beta \) angles have the same measure because they are corresponding interior angles.
The picture illustrates the interior angle property, which states that \(\alpha\) and \(\beta\) are equal.
So how can we implement the two properties discussed above into our diagram of the inclined plane? Looking back at our previous inclined plane diagram, we can identify a right triangle formed by the plane. Since the angle of elevation is \( \theta \), and one of the other angle measures is \( 90^\circ \), we can show that the remaining angle, let's call it \( x \), must measure \( 90-\theta \):
\[\begin{align} & \theta +90+x = 180 \\ & x = 180-90-\theta \\ & x=90-\theta\end{align} \]
Moreover, the two lines in the diagram below, indicated by the purple color, are parallel, so by the interior angle property, we know that both angles indicated as \( 90-\theta \) will be the same.
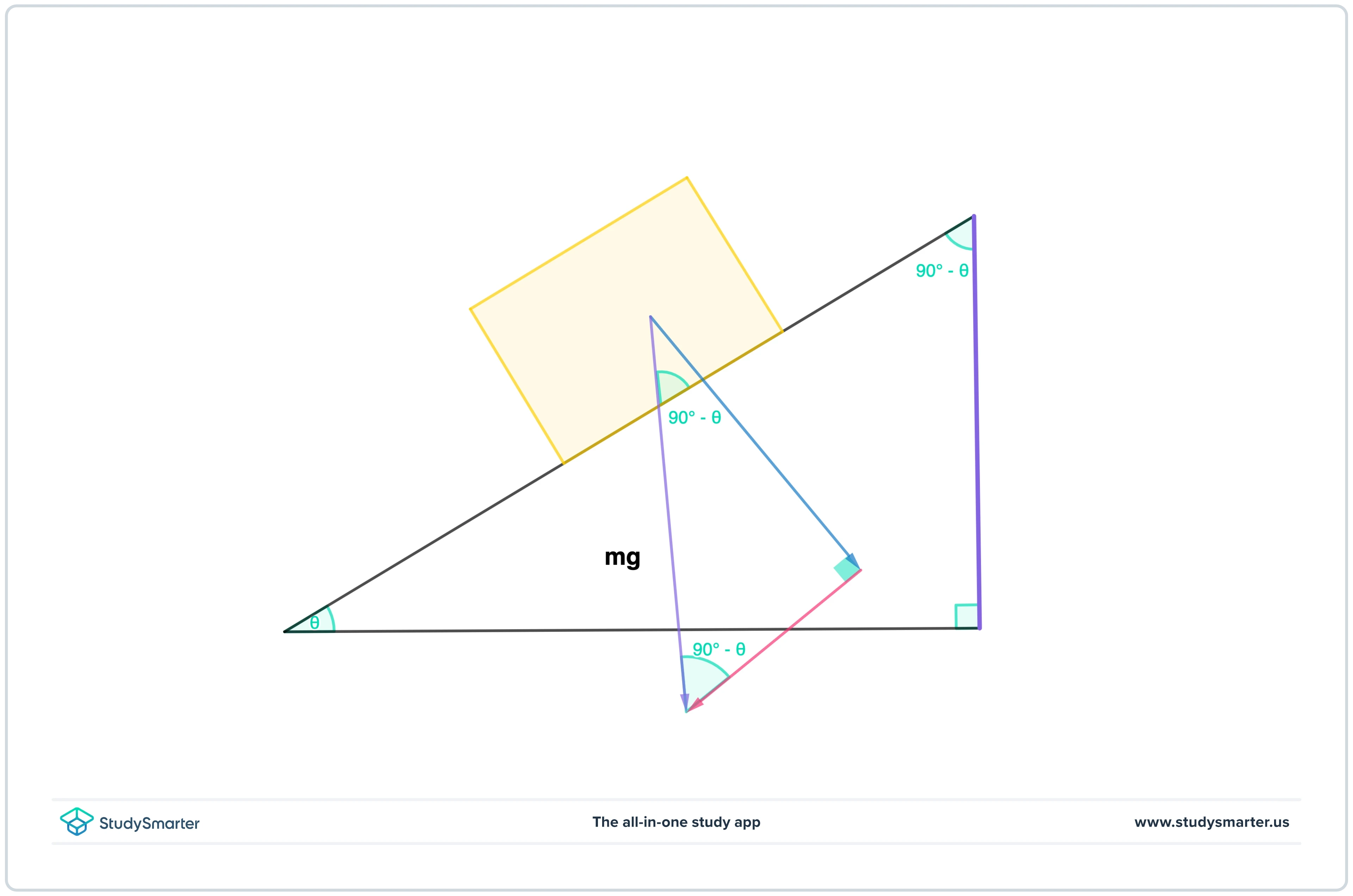
Diagram showcasing the equal angles due to the interior angle rule.
Now that we identified the angle that the box makes with the inclined plane, we can proceed to calculate the angle between the downwards weight force (purple) and its component perpendicular to the inclined plane (blue). We can recognize another right triangle so we can set up an equation for the unknown angle, let's call it \(y\), in a similar way as we did before:
\[\begin{align} y + (90^{\circ} - \theta) + 90^{\circ} &= 180^{\circ} \\[8pt] y &= 180^{\circ} - 90^{\circ} - 90^{\circ} + \theta \\[8pt] y &= \theta \end{align} \]
A right triangle is defined by the weight force and its components.
Perfect! We now have the angle relating to the perpendicular and parallel components of the weight force! Now, we can apply some trigonometry to calculate these components. Recall the definition for the different trigonometric ratios,
\[ \begin{align} \sin(\theta) &= \frac{\text{opposite}}{\text{hypotenuse}} \\[8pt] \cos(\theta) &= \frac{\text{adjacent}}{\text{hypotenuse}}\\[8pt]\tan(\theta) &= \frac{\text{opposite}}{\text{adjacent}} \end{align} \]
Let's first calculate the parallel component (red) from the figure above. Note that the parallel component is the opposite side to the angle \( \theta \). And, since we know the value of the hypotenuse \( (mg) \), we can use the \(\sin(\theta)\) definition. Applying the ratio gives,
\[ \begin{align} \sin(\theta) &= \frac{\text{opposite side}}{\text{hypotenuse}} \\[8pt] \sin(\theta) &= \frac{\text{opposite side}}{mg} \end{align} \]
From here, we can solve for the opposite side and determine the component parallel to the inclined plane.
\[ \text{opposite side} = mg\sin(\theta) = \text{parallel component} \]
Similarly, we can calculate the normal component indicated in blue color by using the definition of \(\cos(\theta)\) as this component is the adjacent side to \( \theta \).
\[\begin{align} \cos(\theta) &= \frac{\text{adjacent side}}{\text{hypotenuse}} \\[8pt] \cos(\theta) &= \frac{\text{adjacent side}}{mg} \end{align} \]
Now, we solve for the adjacent side to determine the normal component.
$$ \text{adjacent side} = mg\cos(\theta) = \text{normal component} $$
The normal and parallel components of the weight force are calculated using trigonometric identities.
Inclined Plane Equation
Now that we've split the weight into its components, we can use Newton's second law to work out the acceleration of the object down the inclined plane. Let's start by doing this for an ideal case and neglect friction for a moment.
A smooth plane is one that presents no effects of friction when considering the motion of the object.
We will first assume we have a smooth plane and ignore the effects of friction. Since the motion of the object is parallel to the inclined plane, we only have to consider the weight component acting in this direction \( mg\sin(\theta) \). Equating this to Newton's second law, we have
\[ \begin{align}F &= ma \\ F=& mg\sin(\theta) \end{align} \]
Thus, the acceleration of the object from rest is
\[ a = g\sin(\theta), \]
where the acceleration, \(a\) is measured in \(\mathrm{m/s^{2}}\) is the acceleration down the plane, \(g\) is the acceleration due to gravity in \(\mathrm{m/s^{2}}\), and \(\theta\) is the angle between the horizontal and the inclined plane measured in degrees.
Friction on an Inclined Plane
In reality, no inclined plane is truly smooth. Therefore, we must consider the effect of friction.
The frictional force is a force that resists the motion between two objects sliding against one another.
The equation for the friction force is given by
\[ F_{f} = \mu r \]
where \(F_{f}\) is the frictional force in newtons (\(N\)), \(r\) is the reaction force (or the normal component of the object's weight) in newtons (\(N\)), and \( \mu \) is the coefficient of friction.
The coefficient of friction is a dimensionless number that quantifies how difficult it is to slide a particular object against a specific surface.
Note that the frictional force always acts opposing the motion of an object. Thus its direction is opposite to that of the motion.
Now, we have two forces we need to consider: the force due to the weight of the object (moving down the plane) and the frictional force opposing the movement (going up the plane). Using Newton's second law, we can write the sum for forces acting on the box as
\[\begin{align} F &= ma\\ mg\sin(\theta) - \mu mg\cos(\theta) &= ma \end{align}\]
where the first term on the left-hand side of the second equation is the weight force down the slope, and the second term is the frictional force going up the slope. Notice that we are resolving our positive direction down the plane so that the frictional force is negative (opposing motion). Now rearranging to isolate the acceleration, we can see that
\[ a = g\sin(\theta) - \mu g\cos(\theta), \]
giving us the acceleration of the object on the inclined plane.
Static Friction vs. Kinetic Friction
It is important to mention that when considering friction on an inclined plane, there are two types: static and kinetic friction. In our previous examples, we assumed that the object on the plane would slide down once we had placed it. However, if the plane had a very rough surface, how can we tell if it would slide down or not? Well, we need to consider the static friction.
Static friction is the friction between two objects when the two surfaces are not moving.
For an object to begin sliding down an inclined plane, it must overcome the static friction between itself and the surface of the inclined plane. However, once it begins moving, the friction tends to be smaller. This is why it is easier to keep moving an object than it is to start moving it. To calculate the friction once the object is in motion, we calculate the kinetic friction.
Kinetic friction is friction between two objects when they are moving with respect to one another.
The way to calculate each of these friction forces is the same: we multiply the normal force times the corresponding coefficient: \( \mu_s \) for static friction or \( \mu_k \) for kinetic friction. In our previous examples, we did not say it explicitly but we were referring to the kinetic friction coefficient for our calculations because we assumed the box was already sliding.
Inclined Plane Examples
Let us consider some examples of inclined plane problems. We have already seen how to find the acceleration of an object on an inclined plane. Let's go a bit farther and see how to find the time it takes for the object to reach the bottom.
Box on an Inclined Plane
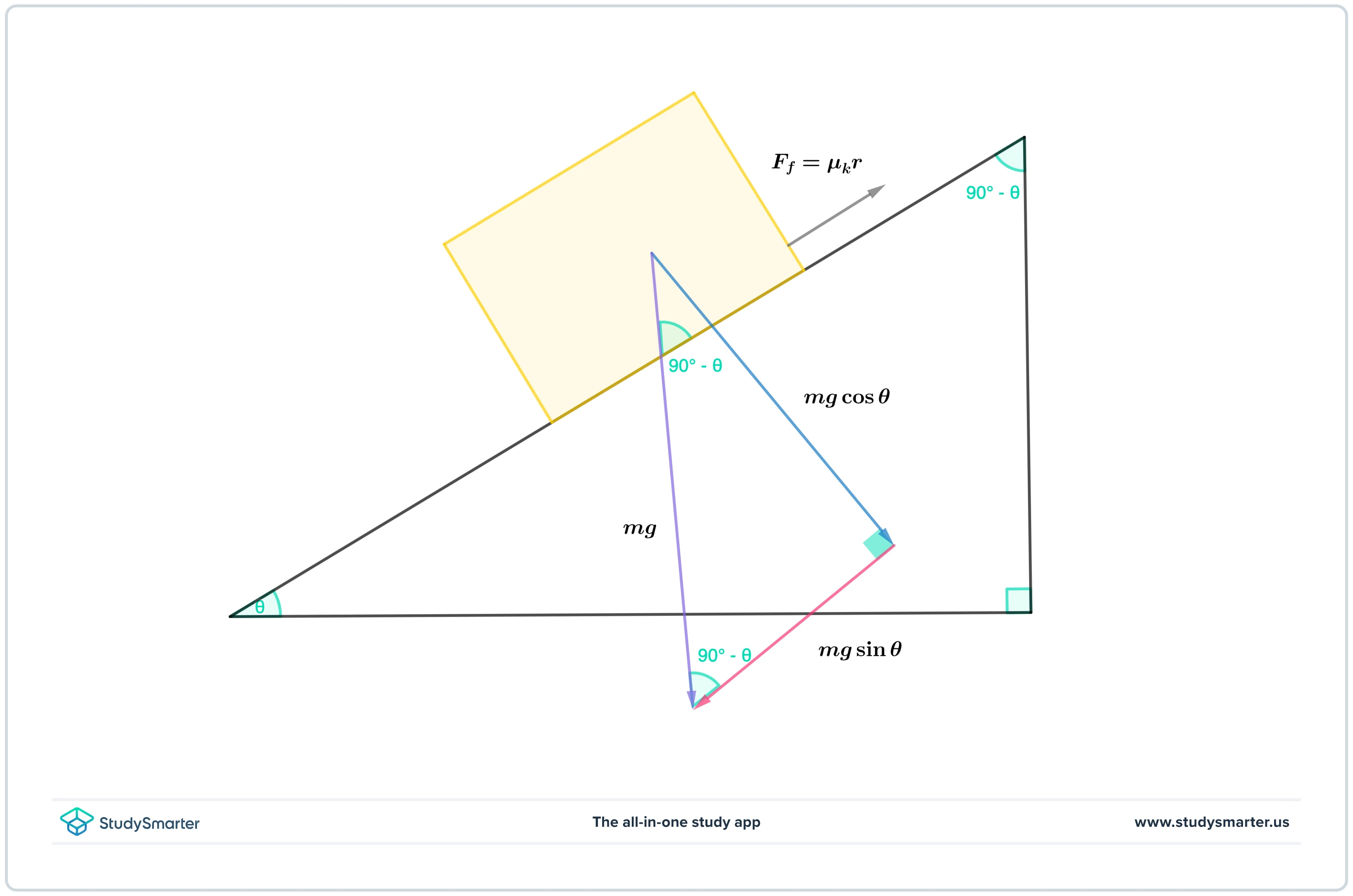
The labeled forces on an inclined plane, forces are either parallel or perpendicular to the plane. Friction is in the opposite direction of motion.
Let us consider the scenario in the diagram above. The values to be used are as follows: \(m = 2.5\; \mathrm{kg}\), \(\theta = 30^{\circ}\), the kinetic friction coefficient is \(\mu_k = 0.3 \), and we take gravitational acceleration as \(g = 9.81\; \mathrm{m/s^{2}}\). Here are assuming that there is friction between the plane and the box but the box still slides down.
The first thing we want to solve is how long it would take for the box to slide all the way to the bottom of the slope. Note that we assume that the objects are moving without slipping. This means that the object's edge moving along the plane remains in contact with the plane for the entire motion. Without this assumption, the problem becomes much more complicated!
Say that the box is placed 5 \(\mathrm{m}\) along the slope from the bottom. This means the box has to travel 5 \(\mathrm{m}\) before its corner touches the floor. We have previously derived the equation to calculate the acceleration of an object placed on a rough inclined plane. Let's plug our numbers into it.
\[ \begin{aligned} a &= g\sin(\theta) - \mu g\cos(\theta)\\ a &= 9.81\;\mathrm{m/s^{2}}\times \sin(30^{\circ}) - 0.3 \times 9.81\;\mathrm{m/s^{2}} \times \cos(30^{\circ})\\ a&= 2.4\;\mathrm{m/s^{2}} \end{aligned} \]
Now that we have our down-the-slope acceleration, we will have to recall our kinematic equations for the motion of objects with constant acceleration to work out how long it will take the box to reach the bottom of the slope. Since we have the distance, initial velocity, and acceleration, and we want to find the time taken, we use
\[ d = v_{i}t +\frac{1}{2}at^{2}\]
and plug in our known values. Our values are as follows \(d = 5\;\mathrm{m}\), \(v_{i} = 0\;\mathrm{m/s}\) (since the object si at rest when placed on the plane), and \(a = 2.4\;\mathrm{m/s^{2}}\).
\[ 5\;\mathrm{m} = \frac{1}{2}\times 2.4\;\mathrm{m/s^{2}} \times t^{2}\]
Now we can solve for \(t\):
\[ t = \sqrt{\frac{2\times 5\;\mathrm{\bcancel{m}}}{2.4\;\mathrm{\bcancel{m}/s^{2}}} } = 2.0s\].
What would happen if the box were pushed down? This is a typical exam question. The only difference is that we need to add the force pushing down the box when calculating the acceleration.
Galileo Inclined Plane Experiment
In the modern day, it might seem common knowledge that all objects accelerate towards the Earth at a constant rate. We refer to this acceleration as the acceleration due to gravity \(g\). However, in the fifteen hundreds, when famous physicist Galileo Galilei was born, it was not a very commonly known fact! In fact, it was ingenious of Galileo to hypothesize that all objects fell at the same rate, so how did he do it?
Technology at the time was not what it is now; there were no super accurate light timers or stopwatches to accurately measure how long it took for an object to fall. Instead, what Galileo used was an inclined plane experiment. Ignoring the effects of friction at the time, he believed that an object accelerating down an inclined plane was no different from an object in free fall. It is just the value of its acceleration which would be slightly different because only a component of this acceleration acts along the plane. With this idea, he was able to prove that all objects accelerated at the exact same rate! The reason why the inclined plane version of the experiment was necessary is due to the limitations of his technology. The versions of timers that were available back in the fifteen hundreds were timepieces such as a water clock. This contraption kept track of time using a steady flow of water into a jug, measuring the difference in water level over an elapsed period of time. Definitely not the most accurate method of measuring time, but hey, it did the job!
Experimental Setup
Galileo measured the time taken for the ball to roll known distances as seen in the diagram.
Referring to the figure above, Galileo used a similar experimental setup, using a ramp and measuring out a range of distances across the entire plane. Then using the water clock as mentioned before, he let the ball roll freely down the ramp, recording the time it took for the ball to cross the various distances. He repeated this experiment multiple times so as to get an average time, making the measurements more precise. This built the basis for good scientific experimentation.
After collecting his data, Galileo found that when the ball rolled a distance four times as long as the first measurement, the time taken was double. He found that this result was consistent across all of the measurements he made, no matter what distances he was using.
Experimental Conclusion
What Galileo drew from this experiment was the relationship between distance and time obeyed
\[ s = \frac{1}{2}at^{2}\]
where \(s\;(\mathrm{m})\) is the distance rolled by the ball, \(a\;(\mathrm{m/s^{2}})\) is the acceleration of the ball, and \(t\;(\mathrm{s})\) is the time taken for the ball to roll. Look familiar? This is because this is the exact kinematic equation we used in the previous section to solve for the time taken for the ball to roll down the ramp when the initial speed of the ball is \(0\;\mathrm{m/s}\).
Galileo then calculated how to relate the acceleration of the ball rolling down the ramp, to the acceleration of the ball if it were in free fall, or gravity as
\[ a = \frac{gh}{l} \]
where \(a\;(\mathrm{m/s^{2}})\) is the acceleration of the ball, \(g\;(\mathrm{m/s^{2}})\) is the gravitational acceleration, \(h\;(\mathrm{m})\) is the height of the ramp, and \(l\;(\mathrm{m})\) is the length of the ramp.
He then combined his two equations, and he was able to solve for gravitational acceleration.
\[ \begin{aligned} s &= \frac{1}{2}at^{2} \\ s &= \frac{1}{2}\left( \frac{gh}{l} \right)t^{2} \\ g &= \frac{2sl}{ht^{2}} \end{aligned} \]
This was revolutionary Physics at the time as Galileo managed to calculate gravitational acceleration with a mere pot of water, ball, and ramp!
By the way, it is worth mentioning that if we consider the ramp elevation angle to be \( \theta \), then the ramp makes a right triangle, just as we discussed before. And here, the height of the ramp \( h \) is the opposite side, and the length \( l \) is the hypotenuse. Then
$$\frac{h}{l} = \frac{\text{opposite side}}{\text{hypotenuse}} = \sin \theta$$
Hence, his expression for acceleration is equal to the one we found for a smooth inclined planed!
\[ a = \frac{gh}{l} =g\frac{h}{l}=g\sin \theta \]
Inclined Planes - Key takeaways
- An inclined plane is a surface elevated at a certain angle in which we consider the motion of an object.
- The weight of the block of mass on an inclined plane can be resolved into a component parallel to the inclined plane and another one perpendicular to it.
- We can use trigonometric ratios to solve for the parallel and perpendicular components of the weight vector.
- The parallel component of the weight is \(mg\sin(\theta)\) and the perpendicular component is \(mg\cos(\theta)\).
- The acceleration of an object down the slope on a smooth surface (without friction) can be represented as \( a = g\sin(\theta)\).
- The frictional force experienced by an object rolling down an inclined plane acts opposing its motion.
- Kinetic friction is only considered when static friction has been overcome and it is calculated as \( F_k = \mu_k r \).
- The acceleration of an object down the slope of a rough surface is given by \( a = g\sin(\theta) - \mu_k g\cos(\theta)\).
References
- Fig. 1 - Slide (https://flickr.com/photos/mrpbps/2877495383/in/photolist-5ogV8n-9VfEUv-cGDBFE-9VFsrv-581XwR-arhEzE-mNoa7w-e754Lg-neEjtB-KzLEL-bND4W-h27U11-py7bEp-SouoQC-dCmLW7-ck85RU-bnySEw-aju5wW-UW4PUC-6eTxGR-7NEbS3-M7M5Z3-p6d28y-dwF7Uz-hinik-87sGFD-bniPYg-99hkgU-8pGZP1-bViKcu-cJYjfd-cH3j9y-57DZA2-fm9tan-pjWi1a-7PCyGp-akc2uD-8s66W3-bpHHV7-8qBgij-2xoSBA-9FbLvC-hTUrXj-7JQp18-afsvsR-AqAwR-21BQDJ2-efzL1i-2UNwJ-EDy1fU) by mrpbps (https://flickr.com/photos/mrpbps/) is licensed by CC BY 2.0 (https://creativecommons.org/licenses/by/2.0/)
Explanations 
Exams 
Magazine 
