What is an arc measure?

An arc measure is the angle from which an arc of a circle subtends.

How do you find the measure of an arc?

How to find the measure of an arc: given the radius and arc length, the arc measure is the arc length divided by the radius. Given the circumference, the ratio between the arc measure and 360 degrees is equal to the ratio between the arc length and the circumference.

What is the formula for finding the arc measure of an arc?

The arc measure is the arc length divided by the radius.

what is the degree measure of an arc

The arc measure is the arc length divided by the radius.

what is arc measures geometry with examples

In geometry, the arc measure is the arc length divided by the radius.

Arc measures: Meaning, Examples & Formula

It is very important to be familiar with the anatomy of a circle and especially the angles within it. This article covers the properties of arc measures, the formula for an arc measure, and how to find it within a geometric context.

The arc and its measure

There are two important definitions to be aware of:

The arc of a circle

An arc is the edge of a circle sector, i.e. the edge bounded/delimited by two points in the circle.

Arc length is the size of the arc, i.e. the distance between the two delimiting points on the circle.

The measure of an arc

If we think of an arc as being the edge between two points A and B on a circle, the arc measure is the size of the angle between A, the centre of the circle, and B.

In relation to the arc length, the arc measure is the size of the angle from which the arc length subtends.

Here are these definitions demonstrated graphically:

Arc measures finding the measure of an arc StudySmarter Finding the measure of an Arc StudySmarter original

Radians versus degrees

Before we introduce the formula for arc measurement, let’s recap degrees and radians.

To convert radians to degrees: divide by $π$ and multiply by 180.

To convert degrees to radians: divide by 180 and multiply by $π$ .

Here are some of the common angles which you should recognise.

Degrees	0	30	45	60	90	120	180	270	360
Radians	0	$\frac{π}{6}$	$\frac{π}{4}$	$\frac{π}{3}$	$\frac{π}{2}$	$\frac{2 π}{3}$	$π$	$\frac{3 π}{2}$	$2 π$

Arc measure and arc length formulae

Finding the arc measure with the radius

The formula that links both the arc measure (or angle measure) and the arc length is as follows:

$S = r \times θ$

Where

r is the radius of the circle
$θ$ is the arc measure in radians
S is the arc length

We can find the arc measure given the radius and the arc length by rearranging the formula: $θ = \frac{S}{r}$ .

Find the arc measure shown in the following circle in terms of its radius, r.

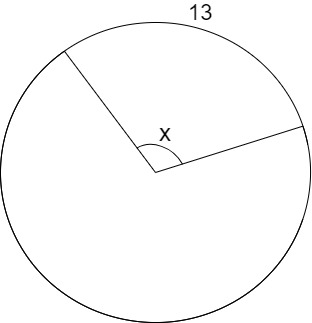
Arc measures Arc measures StudySmarter

Using the formula $S = r \times θ$ :

$13 = r \times x$

We need the arc measure in terms of r, so we need to rearrange this equation:

$x = \frac{13 °}{r}$

Finding the arc measure with the circumference

If we are not given the radius, r, then there is a second method for finding the arc measure. If we know the circumference of a circle as well as the arc length, then the ratio between the arc measure and $360 °$ (or $2 π^{c}$ depending on whether you want the arc measure in degrees or radians) is equal to the ratio between the arc length and the circumference.

$\frac{θ}{360 °} = \frac{S}{c}$

Where

c is the circumference of the circle
$θ$ is the arc measure in degrees
S is the arc length

Find the arc length, x, of the following circle with a circumference of 10 cm.

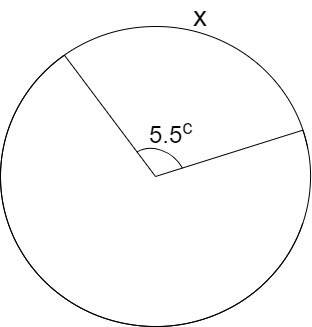
Arc measures finding x StudySmarter

Using the formula $\frac{θ}{2 π} = \frac{S}{c}$ :

$\frac{5.5}{2 π} = \frac{x}{10}$

Rearranging, we get:

$x = 10 \times \frac{5.5}{2 \times π} = 8.75$ to 3 s.f.

Arc Measures - Key takeaways

An arc is the edge of a circle sector, i.e. the edge bounded/delimited by two points in the circle.
Arc length is the size of the arc, i.e. the distance between the two delimiting points on the circle.
An arc measure is the size of the angle from which the arc subtends.
Finding the arc measure given the radius and arc length:
- S=r×θ
  Where
  - r is the radius of the circle.
  - $θ$ is the arc measure in radians.
  - S is the arc length.
Finding the arc measure given the circumference and arc length:
- $\frac{θ}{360 °} = \frac{S}{c}$
  Where:
  - c is the circumference of the circle.
  - $θ$ is the arc measure in degrees.
  - S is the arc length.

Find Study Materials for

Create Study Materials

Arc Measures