The Relationship between Logarithmic functions and exponential functions
The logarithmic function is defined to be the inverse of the exponential function. See Inverse Functions for more details on exactly how functions and their inverses are related, but in short two functions f and g are inverses of each other if
For more information on how functions and their inverses are related, see Inverse Functions .
When you look at the graphs of an exponential function, and the corresponding logarithmic function, they are reflections of each other across the line . In other words, if the point is on one of the graphs, then the point is on the other graph.
 Inverse functions | StudySmarter Originals
Inverse functions | StudySmarter Originals
Logarithmic Function Rules
You will be using the rules of logarithms:
- Product Rule:
- Quotient Rule:
- Reciprocal Rule:
- Power Rule:
- Proportional Rule (Change of Base formula):
Simplify the expression .
Answer:
Step 1: If that were a logarithm base 10 then the answer would be using properties of inverse functions. So the idea is to use the Proportion Rule (also known as the change of base formula) to make it into a base 10 logarithm first. There are two ways to think about doing this, and you get the same answer either way.
The first way to think about it is to use the fact that 10 is the number you are raising to a power to get:
The second way is to look at the logarithm and see that it is base 100, and use that to get:
and then solve for to get that Both methods work, and you can use the one that is easiest for you to understand and remember.
So you have
Step 2: Now using properties of exponents,
So the expression completely simplified is
Common Mistake - Logarithmic Functions
Whenever you use the rules of logarithms, you need to be sure that you use values for x that make sense for the function, as well as the exponential function, since they are inverses.
For example, you can't try and use negative values for in because the exponential function is always positive. A negative x value would make negative (x and y switch with inverses).You also can't use a negative constant for the base in a logarithm because you can't use it as the base of an exponential function.
A logarithmic function is any function of the form where , , and . This is read f(x) equals the log base b of x.
When there is no base b listed, it is taken to be 10. So means the same thing as .
What is the inverse of the function ?
Answer:
Remember that when no base is listed it is taken to be 10. So the inverse of is .
What is the inverse of the function ?
Answer:
Remember that inverses work both ways! So the inverse of is .
List at least 3 points on the graph of without graphing the function or using a calculator.
Answer:
This problem looks trickier than it actually is. You already know that the inverse of is , and that if is a point on the graph of then is a point on the graph of .
Step 1: Exponential functions have a y intercept at , so the point is on the graph of .
Step 2: To get two more points on the graph, evaluate points on the graph of . Choosing two random values, .
Step 3: Evaluate another point on the graph of
Step 4: So the points and are on the graph of . So you know that the points and are points on the graph of .
So without using a calculator, you can see that three points on the graph of are , , and .
Properties of the logarithmic function
Looking at the key takeaway, because the two are equivalent, you can use properties of the exponential function (see Exponential Functions ) when thinking about properties of logarithmic functions. An exponential function can't have a negative number for the base, which is why the base of the logarithmic function can't be negative either. The exponential function only takes on positive values for y, so the logarithmic function only can use positive numbers for x.
This leads to the following properties of logarithmic functions:
- the domain is
- the range is
- there is no y-intercept
- the x-intercept is at
- the vertical asymptote has the equation
Graphing Logarithmic Functions
First let's look at some examples graphed together to see how the base b affects the graph.
Here
 Graphs of logarithms of different bases | StudySmarter Originals
Graphs of logarithms of different bases | StudySmarter Originals
They all
- have the same vertical asymptote at .
- have the same x intercept at .
- are concave down
- are increasing functions.
Let's take a look at the base of the functions in the example and use the change of base formula.
So really they are all just constant multiples of .
What if instead, the base was a fractional power of 2? For example if but now you have
, , and , then
which means that again they are constant multiples of , but they should be flipped over the x axis as well.
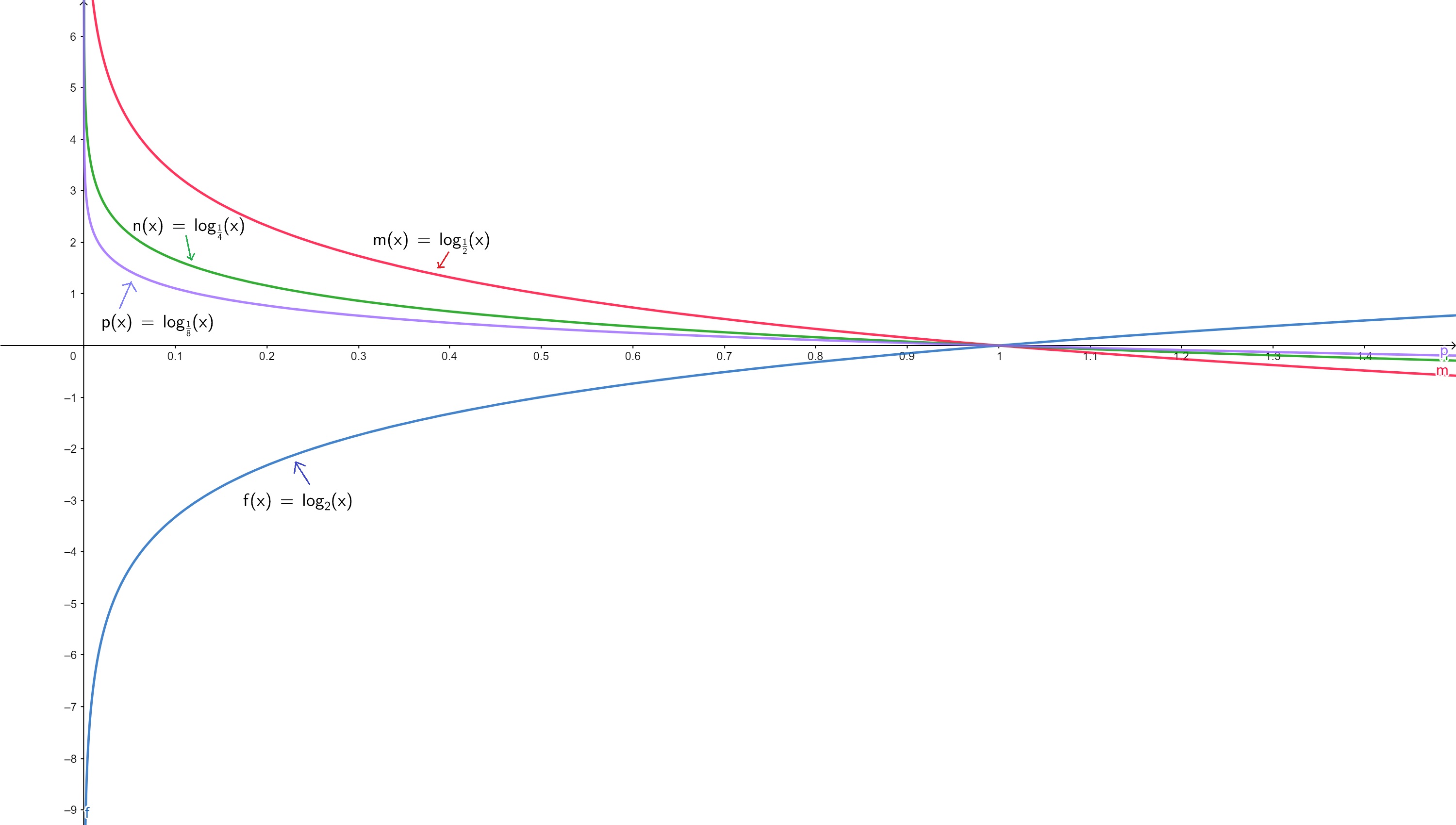
logarithms with fractions as the base | StudySmarter Originals
So as you can see, these three new functions are
- decreasing,
- concave up,
- have as the vertical asymptote, and
- all have the same x intercept at .
Examples of logarithmic functions
Logarithmic functions are used to model things like noise and the intensity of earthquakes. Let's take a look at some real-life examples in action!
Sounds are measured on a logarithmic scale using the unit, decibels (dB). Sound can be modeled using the equation:
Where
- is the power of the sound,
- is the smallest sound a person can hear, and
- is the number of decibels for the power :
Say you are thinking of buying a new speaker. Speaker A says it has a noise rating of 50 decibels, while speaker B says it has a noise rating of 75 decibels. How much more intense is the sound from speaker B than from speaker A?
Answer:
Step 1: For comparison, call the decibel level of speaker A, and the decibel level of speaker B. From the information given, you know that:
- speaker A has where is the power of speaker A
- speaker B has where is the power of speaker B
Step 2: Taking the equation for speaker A and writing it in terms of will let you substitute it into the equation for speaker B. So
Step 3: Substituting this into the equation for speaker B,
So, the sound from speaker B is about 316 times more intense than that of speaker A!
Earthquakes are measured on a logarithmic scale called the Richter scale. The magnitude of an earthquake is a measure of how much energy is released. Here is amplitude of the smallest wave that a seismograph (the device that measures how much the earth is moving) can measure. Then the formula for the Richter scale measurement of an earthquake is
where measures the amplitude of the earthquake wave. In general an earthquake measures between 2 and 10 on the Richter scale. Ones that scores less than 5 on the scale are considered relatively minor, and anything above an 8 on the scale is likely to cause quite a bit of damage. In fact, a magnitude 5 earthquake is 10 times as powerful as a magnitude 4 earthquake.
Suppose that an earthquake in Indiana had a magnitude of 8.1 on the Richter scale, but one on the same day in California was 1.26 times as intense. What was the magnitude of the earthquake in California?
Answer:
Step 1: Using the definition of the Richter scale, and using for the amplitude of the Indiana earthquake, the earthquake in Indiana had
Step 2: Making each side to the base 10 and solving for
:
Now you can use the fact that the California earthquake was 1.26 times as intense as the Indiana one, or in other words, if is the amplitude of the California earthquake, then . So
That means the earthquake in California measured about 8.2 on the Richter scale.
Derivatives of Logarithmic Functions
The derivative of the logarithmic function is
For information on the derivatives of logarithmic functions, see Derivative of the Logarithmic Function.
Logarithmic Functions - Key takeaways
- is equivalent to
- the formula for a logarithmic function is where , and .
- is the same thing as
- logarithms are used in measuring things like decibels and how strong earthquakes are










