Have you ever wondered how you can measure something taller than you, maybe a house or even the tallest building? This question can often be answered with the properties of similar shapes. In this article, we are going to learn about one of the similar shapes called similar triangles.
Similar triangles definition
A similar shape can be described as two shapes that are the same shape, however, they are different sizes.
Similar triangles are a type of similar shape, where two triangles are the same type of triangles but of different sizes.
Similar triangles rules
Two triangles are considered to be similar if they follow these two rules:
- They have the same size corresponding angles.
- All corresponding side lengths have the same ratio.
Similar triangles proof
The idea of similar triangles can be shown and explained in the following diagram:
Example of similar triangles, StudySmarter Originals
Above you can see that the two triangles have a corresponding angle. As well both triangles have sides that are the same ratio. This means that the triangle side lengths are in proportion with one another, the bigger triangle on the right, is 2 times bigger than the smaller triangle on the left. This ratio is also known as a scale factor.
A corresponding angle describes an angle that is the same in both triangles.
There are different theorems that can further prove the idea of similar triangles:
SSS similarity theorem
AA similarity theorem
SAS similarity theorem
SSS similarity theorem
The SSS similarity theorem suggests that when three sides of one triangle are proportional to a corresponding triangle, the triangle is similar.
Example of SSS similarity theorem, StudySmarter Originals
This theorem can be represented in the following formula:
AA similarity theorem
The AA similarity theorem suggests that when the two angles in one triangle are equal to the two angles in another triangle, both triangles are similar.
Example of AA similarity theorem, StudySmarter Originals
This theorem can be represented in the following formula:
SAS similarity theorem
The SAS similarity theorem suggests that when the included angle of one triangle is equal to the included angle of another triangle and the sides length of both triangles are proportional, the triangle will be similar.
Example of SAS similarity theorem, StudySmarter Originals
This theorem can be represented in the following formula:
and
Similar triangles formulas
When looking at similar triangles, they are often made clear to us by using thesymbol. Formulae can be used to show each of the similar triangle theorems:
- When,
- When ,
- When ,
Types of similar triangle examples
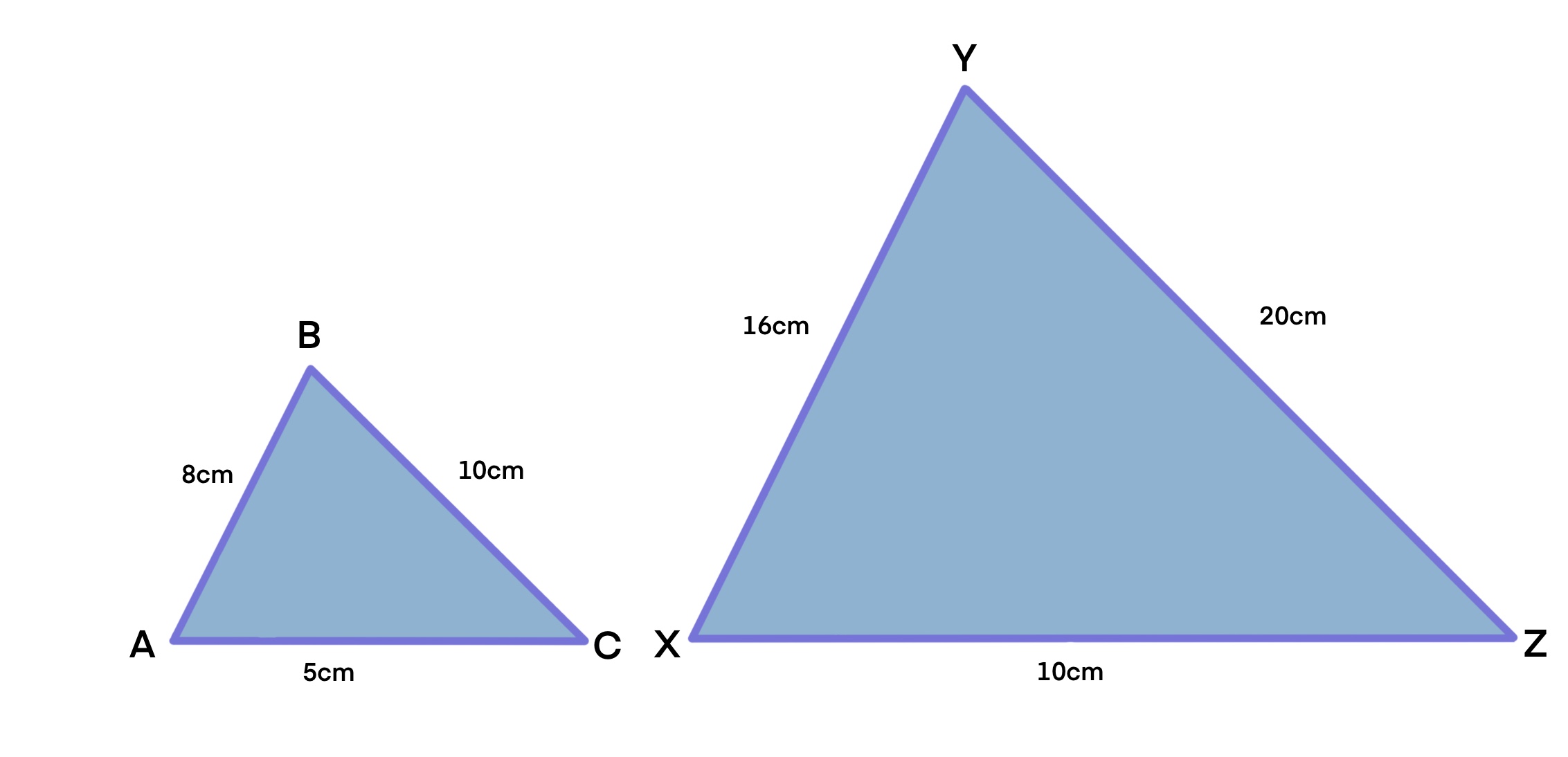
State whether the two triangles below are similar and why.
Example on similar triangles, StudySmarter Originals
Solution:
You can see that the corresponding triangle side lengths are proportional to one another, the bigger triangle on the right is twice as big as the other triangle, which means that they are similar triangles. To prove this we can look at the SSS similarity theorem, which suggests that when you divide the side lengths by their corresponding length you will get the same answer. This then gives you the scale factor. Let's test it:
This proves the SSS similarity theorem, meaning the scale factor is 2.
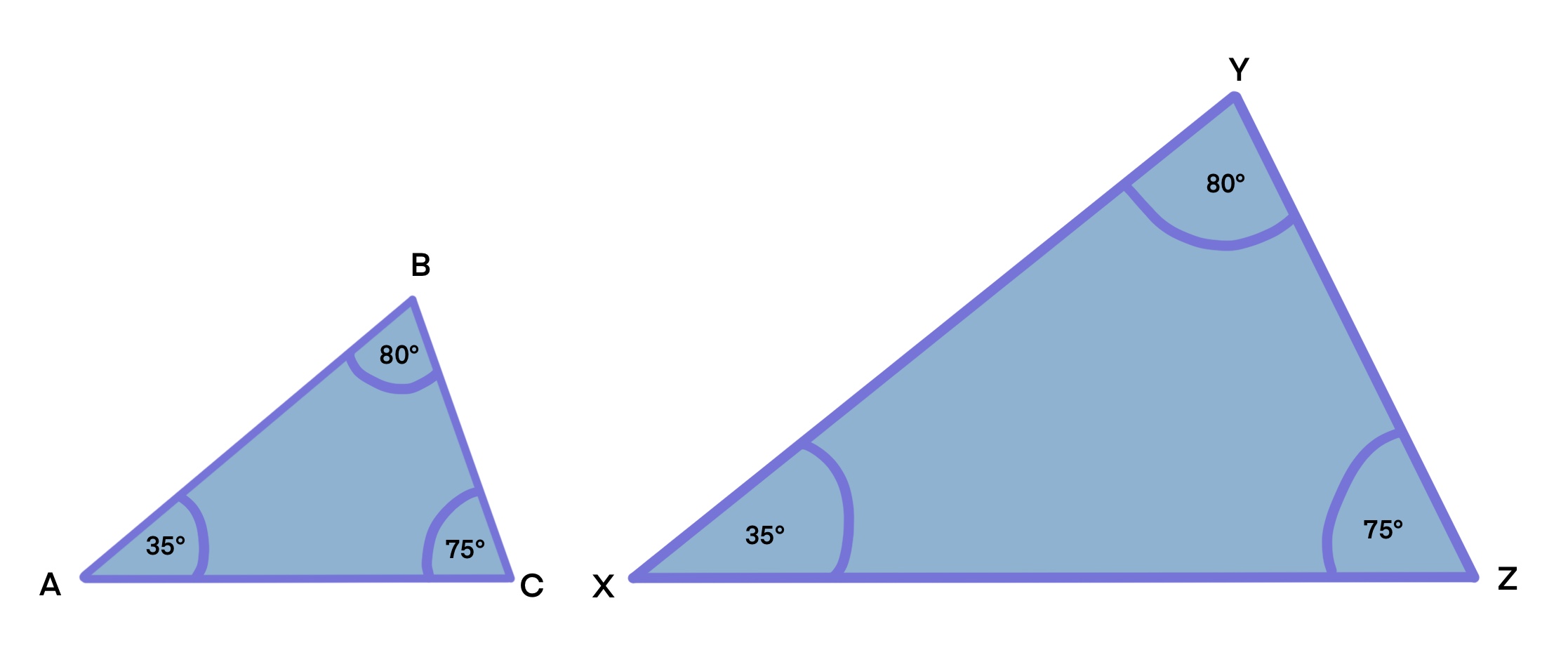
Find the missing angles in these similar triangles:
Example on Similar triangle, StudySmarter Originals
Solution:
Since you have been told that these are similar triangles, you know that the angles correspond with each triangle. Therefore, you know that angle B is 60° and angle X is 45°, you just need to calculate the third angle in the triangles:
This means that both angle C and angle Z are 75°.
Similar Triangles - Key takeaways
- Similar triangles are the same shape but can be different sizes, in order to be considered similar they must either have the same corresponding angles or proportional side lengths.
- There are different theorems to prove whether a triangle is similar:
- SSS similarity theorem
- AA similarity theorem
- SAS similarity theorem
- You can use information from similar triangles to help you find missing angles or side lengths.
Explanations 
Exams 
Magazine 
