The small angle approximation is a trick that can be used to estimate the values of trigonometric functions for small angles measured in radians (small values of![]()
). The small angle approximation is used to make it easier to solve and operate with trigonometric functions.
Small angle approximation equations
There are three equations we can use for the small angle approximation: one for \(\sin \theta\), one for \(\cos \theta\), and one for \(\tan \theta\).
\(\sin \theta \approx \theta\)
\(\cos \theta \approx 1 - \frac{\theta^2}{2}\)
\(\tan \theta \approx \theta\)
Small angle approximation for sin
The assumption that \(\sin \theta \approx \theta\) can be better understood when we look at the graphs of y = x and y = sin x.
A graph showing the lines y=x (red) and y=sin x (blue)
Now, as you can see around x = 0, the graphs of y = x and y = sinx are very close to each other.
A graph showing the lines y=x (red) and y=sin x (blue) around x=0
This is why, for very small angles, we can say that \(\sin \theta \approx \theta\).
Small angle approximation for cos
The approximation for cosine isn't quite as straightforward as for sin. The small angle approximation for cos is derived using the small angle approximation result that we got for sin, and a double angle formula. We use the double angle formula:
\(\cos 2x = 1 - 2 \sin^2 x\)
Now, if we say that \(\cos 2x = \cos \theta\) then \(x = \frac{\theta}{2}\). So, \(\cos \theta = 1- 2 \sin^2\Big( \frac{\theta}{2} \Big)\)
We know from our previous calculation that for a small value of \(\theta\) we assume that:
\(\cos \theta = 1 - 2 \Big(\frac{\theta}{2} \Big)^2\)
Which, simplified, gives us the small angle approximation for cos:
\(\cos \theta \approx 1 - \frac{\theta^2}{2}\)
Small angle approximation for tan
For the small angle approximation of tan, we use the same logic as for sin. Looking at the graphs of y = tanx and y = x,
A graph showing the lines y=x (red) and y=tan x (blue)
Again, for values close to x = 0, we see that the two functions are very close to each other:
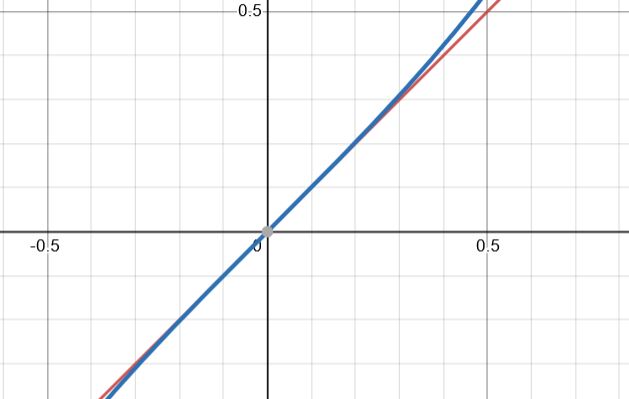
A graph showing the lines y=x (red) and y=tan x (blue) around x=0
Hence, we assume that for small values of \(\theta, \space \tan \theta \approx \theta\)
How to solve questions using the small angle approximation
The formulas derived earlier can be used in questions and problems to make it easier and quicker to solve them. We will look at a few examples of how to apply this.
When \(\theta\) is small, show that \(\frac{\cos \theta}{\sin \theta}\) can be approximated by \(\frac{2 - \theta^2}{2 \theta}\).
To solve this question, we will need to use the small angle approximations for sin and cos: \(\sin \theta \approx \theta, \cos \theta \approx 1 -\frac{\theta^2}{2}\). We can now substitute this into \(\frac{\cos \theta}{\sin \theta}\), which gives us \(\frac{1-\frac{\theta^2}{2}}{\theta}\). We can simplify this expression by multiplying top and bottom by 2: \(\frac{2-\frac{2\theta^2}{2}}{ 2\theta}\) which simplifies to \(\frac{2-\theta^2}{2 \theta}\), as required by the question.
a) When x is small, show that tan (3x) cos (2x) can be approximated by \(3x - 6x^3\)
b) Hence approximate the value of tan (0.3) cos (0.2) to 3 sf
This question needs to be answered in two parts: a and b. Let's start by looking at how we would solve a). We will need to use the facts did tan x≈ x and \(\cos x \approx 1 - \frac{x^2}{2}\). Substituting this into tan (3x) cos (2x), we get: \(3x \Big(1- \frac{(2x)^2}{2} \Big)\)or \(3x(1-2x^2)\). Multiplying the bracket by 3x: \(3x-6x^3\) as required.
For part b, we have to find the tan value for 0.3 and cos for 0.2. We know the expressions for tan 3x and cos 2x, so: 3x = 0.3 and 2x = 0.2 gives us x = 0.1. Now we can plug in 0.1 into the expression we found earlier: \(3 (0.1) - 6(0.1)^3 = 0.294\)
If the angle is given in degrees, you will need to convert it to radians first to use the small angle approximation. You can use the formula \(radian = degree \cdot \frac{\pi}{180}\)
Small Angle Approximation - Key takeaways
The small angle approximation can be used to make it easier to work with trigonometric functions when looking at angles close to 0 rad.
The small angle approximation has to be worked out in radians.
The three formulas for small angle approximation are:
\(\sin \theta \approx \theta, \tan \theta \approx \theta ,\cos \theta \approx 1 - \frac{\theta^2}{2}\)
Explanations 
Exams 
Magazine 
